EP 4 of the ulab library is about the linalg submodule used for linear algebra calculations which is applied to solve linear problems. And it is a tool to predict or study the nature of what happens in a linear way. This article discusses the functions of the linalg submodule and some basic usage examples.
linalg
The linalg submodule is a linear algebraic operation that supports calculations for matrix inversion, dot product, determinant, eigenvalues, eigenvectors, Cholesky decomposition and trace calculations. The use of the functions is as follows.
- result = ulab.linalg.cholesky( A ) Used to solve linear equations Ax = b if matrix A is symmetric square matrix and positive definite matrix which is commonly used for linear least square linear equation, the partial differential equation, which is used in the Monte Carlo method and as a tool in the study of finance. But if matrix A is not square matrix and positive definite matrix, it will cause a malfunction.
- result = ulab.linalg.det( M ) Find the determinant of matrix M
- result = ulab.linalg.dot( M, N ) Calculate the dot product between the M and N matrix.
- eigenvalues,eigenvectors = ulab.linalg.eig( M ) Calculates the eigenvalues and the eigenvectors of a real, symmetric square matrix. If the matrix is not symmetric, a ValueError will be raised.
- result = ulab.linalg.inv( M ) Find the reciprocal or inverse of the square matrix. If an error occurs, the error can be detailed from the ValueError, and it is crucial to note that calculating the reciprocal of the matrix need to uses a large amount of memory to store float-type matrixes.
- result = ulab.linalg.norm( M ) Used to find the square root of the sum of squares of the members within an array.
- result = ulab.linalg.size( n ) Returns the conditional size of n, i.e.
n = 0 Returns the number of elements in an array.
n = 1 Returns the number of rows.
n = 2 Returns the number of columns. - result = ulab.linalg.trace( M ) Find the sum of the diagonal members of a rectangular matrix.
Example 1
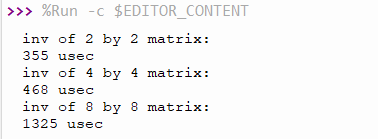
The example code18-8 calculates the reciprocal matrix sizes 2×2, 4×4 and 8×8. The result of the operation is shown in Figure 1. We found that the larger the matrix size, the more time required to compute.
#code18-8
import ulab as np
import time
print('inv of 2 by 2 matrix:')
m = np.array([[2, 1], [3, 5]])
t0 = time.ticks_us()
np.linalg.inv(m)
print("{} usec".format(time.ticks_us()-t0))
print('inv of 4 by 4 matrix:')
m = np.array([[7, 2, 1, 4], [5, 5, 4, 4], [0, 2, 8, 3], [8, 0, 3, 1]])
t0 = time.ticks_us()
np.linalg.inv(m)
print("{} usec".format(time.ticks_us()-t0))
print('inv of 8 by 8 matrix:')
m = np.array([[ 1, 2, 3, 4, 5, 6, 7, 8],
[ 9,10,11,12,13,14,15,16],
[21,18,19, 0,21,22, 0,10],
[33, 0, 1, 0,29, 0,31,10],
[49,34,35,36,37,38,39,10],
[ 1, 1, 0,44,45, 0,47,10],
[49, 0,51,52,53,54, 0,10],
[ 1,58,59, 0,61, 0,63,10]])
t0 = time.ticks_us()
np.linalg.inv(m)
print("{} usec".format(time.ticks_us()-t0))
Conclusion
From this article, we found that the function of the linalg submodule is the computation of the matrix to solve linear algebraic problems. Most of them have conditions of use that must be careful because using an incorrect matrix will result in a program crash. Therefore, coding instructions should intercept errors in the following format to report the type of error that has occurred.
try:
…instructions…
except ValueError as e
print(“{}”.format(e))or
try:
… instructions…
except IndexError as e:
print(“{}”.format(e))
Finally, have fun with programming.
Reference
(C) 2020, By Jarut Busarathid and Danai Jedsadathitikul
Updated 2021-08-16