EP 8 is the final part ulab series, a mathematical library that can be used for AI. This chapter discusses the poly, fft, and filter submodules which explain how each function works with examples of usage to guide for further application.
poly
The poly submodule is a group of functions used for polynomial calculations, which are expressions made up of one or more variables and coefficients. It performs operations with methods of addition, subtraction, multiplication, or exponentiation (must be a non-negative integer exponent only). The commands supported by the submodule are the same as numpy namely:
- result = ulab.poly.polyval( p, x) It evaluates a polynomial, which requires two arguments to be an array and a resulting array is formed by multiplying the value in x by all members of p and raising the power of x by the sequence of exponents. 2*3^2+4*3^1+2*3^0 must create p as an array of [2, 4, 2] and let x be 3.
- polyfit( x, y, a ) Non-linear regression is calculated, where x is an array of independent variables, y is an array of dependent variables, where the number of elements of x and y must be equal, and a is the degree of the polynomial.
- polyfit( y, a ) This is a non-linear regression, where y is the array of dependent variables and a is the degree of the polynomial.
Example Code 1
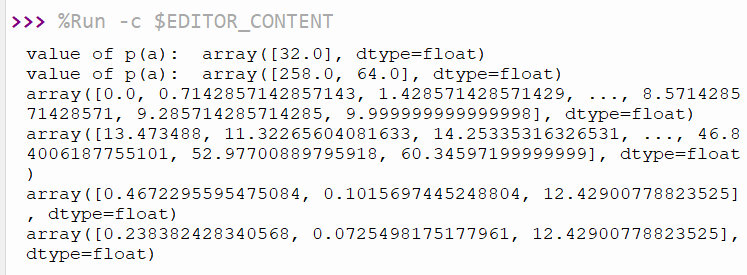
The example code18-16 is an example of using polyval and polyfit to calculate values. The result is shown in Figure 1.
# code18-16 : poly
import ulab as np
import esp32
import time
# 2*3^2+4*3^1+2*3^0 = ?
p = np.array([2,4,2])
a = np.array([3])
print('value of p(a): ', np.poly.polyval(p, a))
# 2*3^4+3*3^3+1*3^2+2*3^1+0*3^0 = ?
# 2*2^4+3*2^3+1*2^2+2*2^1+0*2^0 = ?
p = np.array([2,3,1,2,0])
a = np.array([3,2])
print('value of p(a): ',np.poly.polyval(p, a))
x = np.linspace(0,10,15)
y = np.array([0]*15,dtype=np.float)
for idx in range(15):
y[idx] = (x[idx]*x[idx])/2.0+(esp32.hall_sensor()*(time.ticks_ms()/1000000.0))
print(x)
print(y)
print(np.poly.polyfit(x,y,2))
print(np.poly.polyfit(y,2))
fft
The fft submodule is used to calculate the transform with the fast Fourier method and the transform inverse also supports the functionality of the spectrogram function as well as the scipy library.
- realNumber, imaginaryNumber = np.fft.fft(x) Convert Fourier of array x to a value in the frequency domain.
- realNumbers, imaginaryNumbers = np.fft.fft(x,y) Convert Fourier of arrays x and y to values in the frequency domain.
- array1, array2 = np.fft.ifft( real array, imaginary array ) Finds the reciprocal of the Fourier transform.
- spectrogram(x) Finds the sum of the square root of a real squared number and an imaginary square obtained from fft of x.
Example Code 2
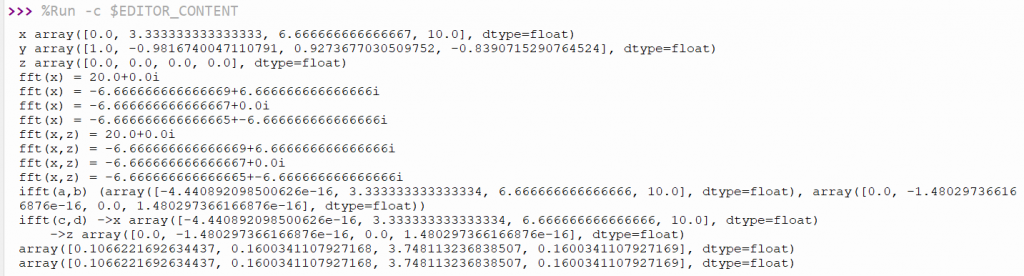
The example code18-17 is an example of the function fft, ifft, and spectrogram. The result is shown in Figure 2.
#coce18-17 : fft
import ulab as np
# FFT
numData = 4
x = np.linspace(0,10,numData)
print("x",x)
y = np.vector.cos(x)
print("y",y)
z = np.zeros(len(x))
print("z",z)
a,b = np.fft.fft(x)
for i in range(numData):
print("fft(x) = {}+{}i".format(a[i],b[i]))
c,d = np.fft.fft(x,z)
for i in range(numData):
print("fft(x,z) = {}+{}i".format(c[i],d[i]))
#
xnew = np.fft.ifft(a,b)
print("ifft(a,b)",xnew)
x2new,znew = np.fft.ifft(c,d)
print("ifft(c,d) ->x",x2new)
print(" ->z",znew)
#
a,b = np.fft.fft(y)
s = np.fft.spectrogram(y)
print(np.vector.sqrt(a*a+b*b))
print(s)
filter
The filter submodule supports the convole function to perform convolutions with the 1D array. It supports the cascaded second-order filtering function with the sosfilt function as in the scipy library.
- result = np.filter.convolve( x, y ) Returns the discrete value of the linear convolution of two 1D arrays.
Example Code 3
The example code18-18 uses the convolve function of the filter submodule. The result of convolving between x and y is shown in Figure 3.
#coce18-18 : filter
import ulab as np
x = np.array([1,2,3,4,5])
y = np.array([1,10,100,1000])
print("x convolute with y = {}".format(np.filter.convolve(x,y)))

Conclusion
In this article, readers get to know the functions of poly, fft and filter submodules, along with explanations and examples of programs. The authors hope that this will be a guideline for further implementation. More importantly, the functionality can be applied to Python’s numpy library except for fft where the reader must convert real numbers and Imaginary numbers because ulab doesn’t support the use of complex numbers.
Finally, we hope readers will continue to enjoy programming.
Reference
(C) 2020, By Jarut Busarathid and Danai Jedsadathitikul
Updated 2021-08-23