For ESP8266’s MicroPython to perform mathematical calculations like using Python’s numpy library, MicroPython with ulab must be installed. You can download firmware for ESP8266 HERE. For normal ESP32 and with additional PSRAM (SPIRAM).
This article is an introduction to ulab and an overview of the libraries within ulab for further application.
ulab
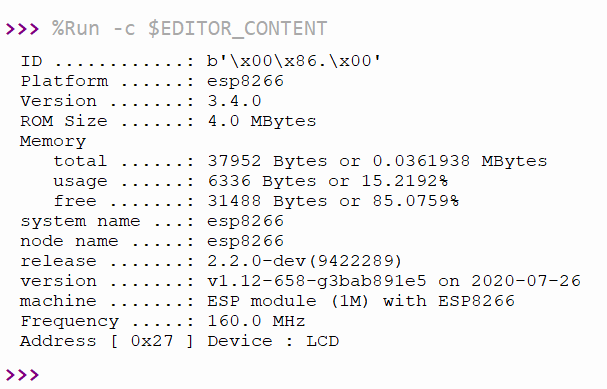
ulab is an array manipulation library written in C to create a Python numpy functional library, but it is designed primarily for MicroPython and can be compiled for use with ESP8266, ESP32, CircuitPython, SAMD51/nRF, MicroPython for K210, MaixPy, OpenMV and PyCom. In this article, we choose ESP8266 with more than 1MB of ROM to enable double-precision decimal. First, download firmware and write firmware with ESP8266 and execute code from the previous article will be resulted as Figure 1.
The list of functions and submodules of ulab is shown in Figure 2. It is found that ulab has functions and submodules available ie. array, linalg, vector, numerical, poly, fft, filter, compare and approx. As for the ‘user’ section is a section for users to create themselves.

All ulab-generated arrays are of the same type, and the ulab implementation starts with import command as follows:
import ulab
The list of available functions of ulab is as follows.
- set_printoptions(threshold=10, edgeitems=3)
Sets threshold and edgeitems, where threshold is the amount of data to display in the print statement when the amount of data to display is greater than the threshold, the edgeitems are displayed on the front and rear and “…” displayed in the middle. For example, set threshold to 10, but the amount of data is 20 consisting of integers 1 to 20 and edgeitems set to 2, the data to display will be 1, 2, …, 19, 20. - get_printoptions()
Tells the values of thresholds and edgeitems that are set. - arange( n, dtype=ulab.uint16 )
To create a dtype 1-dimensional array with n members, each with values from 0 to n-1. - arange( start, stop, dtype=ulab.int16)
To create a dtype 1-dimensional array with number of members from start to stop, with each member having a value from start to stop-1. - arange(start, stop, step, dtype=ulab.int16)
To create dtype 1-dimensional array with number of ((stop-start)/step) members, each member having values from start to stop-1, each step apart. - eye( n, dtype=ulab.float )
For generating dtype identity matrix arrays of n rows * n columns. - linspace( start, stop, n )
To create a 1-dimensional array of n members, where the firstelement is start and the last is stop. The members between the first and last members are calculated from the linear equation.
Note: When used with an integer with the number of n is greater than the distance between the start and stop values will result in a miscalculation and the program stops working. - ones((row, col),dtype=ulab.float)
To create an dtype array with size of row * column where every element has a value of 1. - zeros((row, col),dtype=ulab.float)
To create an dtype array with size of row * column where every element has a value of 0.
Example 1
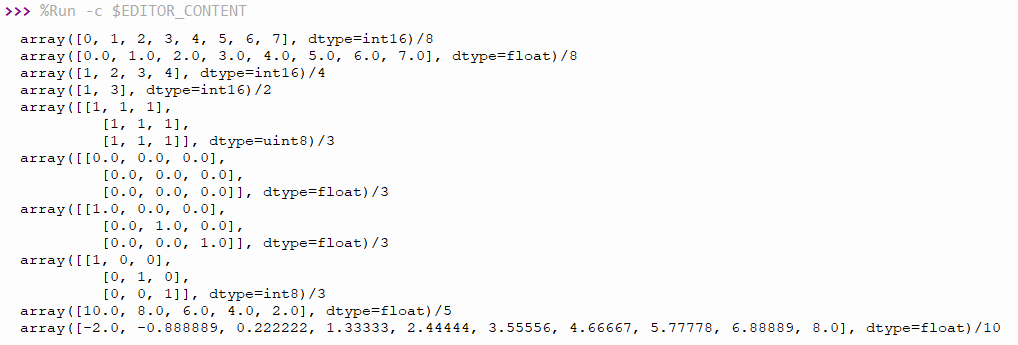
The code18-1 sample program is an experiment with ulab to create a basic array and matrix. and the result is as shown in Figure 3.
# code18-1
import ulab as np
a = np.arange(8)
b = np.arange(8,dtype=np.float)
c = np.arange(1,5)
d = np.arange(1,5,2)
e = np.ones((3,3),dtype=np.uint8)
f = np.zeros((3,3))
g = np.eye(3)
h = np.eye(3, dtype=np.int8)
i = np.linspace(10,2,5)
j = np.linspace(-2, 8, 10)
print("{}/{}\n{}/{}".format(a,len(a),b,len(b)))
print("{}/{}\n{}/{}".format(c,len(c),d,len(d)))
print("{}/{}\n{}/{}".format(e,len(e),f,len(f)))
print("{}/{}\n{}/{}".format(g,len(g),h,len(h)))
print("{}/{}\n{}/{}".format(i,len(i),j,len(j)))From code18-1 we can find that
- The variable a is created by creating an array variable of 8, so it has 0 to 7 elements and has a total of 8 elements.
- The variable b is created by creating a decimal array variables of 8, each of which is 0.0 to 7.0, and has a total of 8 elements.
- The variable c is created by defining a starting and an ending point therefore the first element is 1 and the last is 5-1 or 4 so there are 4 members total.
- The variable d is created by defining a starting and ending point and increasing/decreasing values between each value therefore the initial value is 1, followed by (1+2) or 3, but the next one when adding another 2 over the range. Thus ended the creation of members just like this.
- The variable e creates a matrix (2D arrays) of 3 rows * 3 columns, with each member holding a value of 1. If observed, len() returns 3 because there are 3 rows of data. when you added command print(“len: e[0]={} e[1]={} e[2]={}”.format(len(e[0]), len(e[1]), len(e[ 2]) )) will found that each row has 3 elements.
- The variable f creates a 3*3 matrix with each element being 0.0.
- The g variable creates a 3*3 identity matrix.
- he variable h creates a 3×3 identity matrix with the int8 data type.
- The variable i generates an array starting from the value 10 and the last value 2, and only needs to create 5 elements.
The variable j creates a variable that starts from the value -2 and the lasts 8 and requires 10 elements.
The types of data that are compatible with ulab are uint8, int8, uint16, int16, and float. The individual ulab submodules are described in the next article.
Example 2
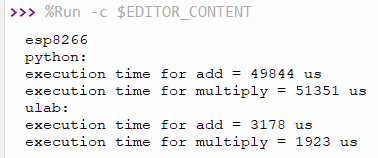
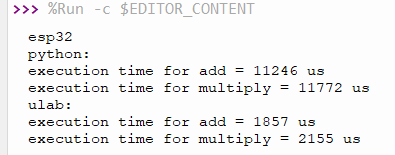
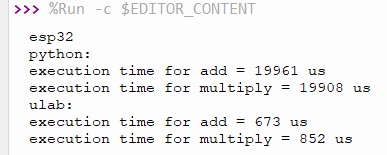
Example of working speed comparison between addition and multiply the array of 1000 members by coding with Python and using ulab as code18-1a and the result from working with ESP8266 is as shown in figure 4 and ESP32 (with PSRAM and without PSRAM) is as shown in the figure 5 and 6.
# code18-0 : Benchmark
import time
import ulab as np
import sys
print(sys.platform)
a = [0.0]*1000
b = range(1000)
print('python:')
t0 = time.ticks_us()
[a[i]+b[i] for i in range(1000)]
print("execution time for add = {} us".format(time.ticks_us()-t0))
t0 = time.ticks_us()
[a[i]*b[i] for i in range(1000)]
print("execution time for multiply = {} us".format(time.ticks_us()-t0))
a = np.linspace(0, 10, num=1000)
b = np.ones(1000)
print('ulab:')
t0 = time.ticks_us()
a+b
print("execution time for add = {} us".format(time.ticks_us()-t0))
t0 = time.ticks_us()
a*b
print("execution time for multiply = {} us".format(time.ticks_us()-t0))
Concusion
From this article, we founded that ulab allows us to write programs or develop programs to process data in 1D or 2D arrays, enabling the ability to expand the capabilities of the microcontroller to work more broadly, such as being used in computations for the rotation of both 2D and 3D objects, statistically calculate, converts to other formats to determine signal characteristics, or used in calculating trends by various methods, which is the basis for putting a small brain into devices like ESP8266/ESP32.
And by comparing the speed of adding and multiplying 1000 data with normal python coding and using ulab, it is found that the speed of ulab is higher, and it is worth noting that the ESP32 without PSRAM installed is faster than ESP32 with PSRAM because PSRAM is the RAM memory connected via the SPI bus which is slower than the speed of internal memory. The ESP32 takes more time to compute with external memory, so if you emphasis on speed, the ESP32 without external memory runs much faster. But the amount of memory available to use is less. Therefore, it must be decided according to the situation, for example, there is a larger amount of data than a normal ESP32 can store or can be processed, you have to choose the one with PSRAM, but if it is used with the data that the ESP32 normally stores. you should choose to use a normal ESP32 to work. due to higher speed and cheaper, etc.
In EP1, this has been introduced to the functions, installation and basic usage. Next time, it will be about sub-modules, arrays, and their usage. Finally, we hope that this article will be a great article for anyone interested in Python programming and applied further. Have fun programming.
(C) 2020, By Jarut Busadathid and Danai Jedsadathitikul
Updated 2021-08-11